Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
Многогранником называют пространственное тело, ограниченное плоскими многоугольниками.
Многоугольники называют гранями многогранника, стороны многоугольников – ребрами многогранника, а вершины многоугольников – вершинами многогранника.
Многогранник называют выпуклым, если он расположен по одну сторону от плоскости каждой из его граней.
Правильным многогранником называют выпуклый многогранник, у которого все грани – правильные многоугольники с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.
Грани правильного многогранника могут быть или равносторонними треугольниками, или квадратами, или правильными пятиугольниками.
Если у правильного многогранника грани – правильные треугольники, то соответствующими многогранниками являются правильный тетраэдр – он имеет 
грани (рис.9.27), правильный октаэдр – он имеет 
граней (рис.9.28), правильный икосаэдр – он имеет 
граней (рис. 9.29).
грани (рис.9.27), правильный октаэдр – он имеет граней (рис.9.28), правильный икосаэдр – он имеет граней (рис. 9.29). Если у правильного многогранника грани – квадраты, то многогранник называется кубом или гексаэдром – он имеет 
граней (рис. 9.30).
граней (рис. 9.30). Если у правильного многогранника грани – правильные пятиугольники, то многогранник называется додекаэдром – он имеет 
граней (рис. 9.31).
граней (рис. 9.31).Сечения многогранников
Секущей плоскостью многогранника называют плоскость, разделяющую этот многогранник на два многогранника. Сечением многогранника называют многоугольник, вершины которого лежат на ребрах многогранника, а стороны – на его гранях.
На рисунке 9.32 плоскость 
– секущая плоскость призмы, а четырехугольник 
– сечение призмы.
– секущая плоскость призмы, а четырехугольник – сечение призмы. Пример 1. Постройте сечение, проходящее через сторону 
нижнего основания и противоположную вершину 
верхнего основания усеченной треугольной пирамиды, изображенной на рисунке 9.33.
нижнего основания и противоположную вершину верхнего основания усеченной треугольной пирамиды, изображенной на рисунке 9.33. Решение. Поскольку точки 
и лежат в грани 
, то 
– прямая, по которой секущая плоскость пересекает эту грань (рис. 9.34). Поскольку точки и
лежат в грани 
, то секущая плоскость пересекает эту грань по прямой 
. Следовательно, треугольник 
– искомое сечение.
и лежат в грани , то – прямая, по которой секущая плоскость пересекает эту грань (рис. 9.34). Поскольку точки и лежат в грани , то секущая плоскость пересекает эту грань по прямой . Следовательно, треугольник – искомое сечение. Пример 2. Постройте сечение, проходящее через точку 
параллельно плоскости основания треугольной пирамиды, изображенной на рисунке 9.35.
параллельно плоскости основания треугольной пирамиды, изображенной на рисунке 9.35.Решение. В плоскости грани 
параллельно прямой построим отрезок 
(рис. 9.36). В плоскости грани 
параллельно прямой 
построим отрезок 
. Так как точки и принадлежат грани 
, то, соединив их, получим треугольник 
– искомое сечение.
параллельно прямой построим отрезок (рис. 9.36). В плоскости грани параллельно прямой построим отрезок . Так как точки и принадлежат грани , то, соединив их, получим треугольник – искомое сечение.Пример 3. Постройте сечение пирамиды 
плоскостью, проходящей через точки 
, , 
и 
, принадлежащие его ребрам 
, 
, 
и 
(рис. 9.37).
плоскостью, проходящей через точки , , и , принадлежащие его ребрам , , и (рис. 9.37).Решение. 1. Поскольку точки 
и 
принадлежат грани 
пирамиды, то, соединяя их, получим отрезок 
, по которому секущая плоскость пересекает эту грань (рис. 9.38).
и принадлежат грани пирамиды, то, соединяя их, получим отрезок , по которому секущая плоскость пересекает эту грань (рис. 9.38). 2. Соединив точки и 
, получим отрезок, по которому секущая плоскость пересекает грань 
. Прямая 
пересекает прямую в точке 
.
и , получим отрезок, по которому секущая плоскость пересекает грань . Прямая пересекает прямую в точке .3. В плоскости грани построим прямую 
, которая прямую 
пересекает в точке 
.
построим прямую , которая прямую пересекает в точке . 4. Соединяя точки и 
, а также точки 
и , получим пятиугольник 
– искомое сечение.
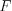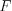и , а также точки и , получим пятиугольник – искомое сечение.Пример 4. Постройте сечение прямого параллелепипеда 
плоскостью, проходящей через точки , и , принадлежащие его ребрам 
, 
, 
(рис. 9.39).
плоскостью, проходящей через точки , и , принадлежащие его ребрам , , (рис. 9.39). Решение. 1. Поскольку точки и принадлежат грани 
параллелепипеда, то, соединяя их, получим отрезок , по которому секущая плоскость пересекает эту грань (рис. 9.40).
и принадлежат грани параллелепипеда, то, соединяя их, получим отрезок , по которому секущая плоскость пересекает эту грань (рис. 9.40). 2. Соединив точки и , получим отрезок, по которому секущая плоскость пересекает грань 
. Прямая пересекает прямую в точке , а прямую 
– в точке .
и , получим отрезок, по которому секущая плоскость пересекает грань . Прямая пересекает прямую в точке , а прямую – в точке .3. В плоскости грани 
построим прямую 
, которая прямую пересекает в точке 
, а ребро параллелепипеда 
– в точке .
построим прямую , которая прямую пересекает в точке , а ребро параллелепипеда – в точке . 4. В плоскости грани построим прямую 
, которая пересечет ребра и в точках 
и 
.
построим прямую , которая пересечет ребра и в точках и .5. Шестиугольник 
– искомое сечение.
– искомое сечение.При построении сечений многогранников необходимо помнить:
а) соединяя точки, лежащие в плоскости одной грани, получим прямую, по которой секущая плоскость пересекает эту грань;
б) если секущая плоскость пересекает две параллельные грани, то линии пересечений параллельны.